• ManFromEarth
• Astronomie + Physik, Sterngeschichten, Video, Wissenschaft
• 0
• 230

Wie lang ist die Küste von Großbritannien? Das klingt nach einer dummen Frage. Immerhin ist Großbritannien ja ein ziemlich großes, ziemlich stabiles Ding. Eine Insel, und keine Wolke oder sonst irgendein flüchtiges Objekt. Eine Insel hat eine Küste, die einmal rundherum geht und diese Küste muss eine bestimmte Länge haben.

Aber manchmal sind dumme Fragen nicht dumm und einfache Dinge komplizierter als man denkt. Die Küstenlänge von Deutschland wird zum Beispiel je nach Quelle mal mit 1200 Kilometer und mal mit 2389 Kilometer angegeben. Die Länge der Grenze von Österreich wird vom CIA World Factbook mit 2524 Kilometer angegeben, vom österreichischen Bundesamt für Eich- und Vermessungswesen dagegen mit 2706 Kilometer. Immerhin ein Unterschied von 182 Kilometer! Das liegt natürlich an unterschiedlichen Meßmethoden, Definitionen und verwendeten Datenbanken. Aber es weist trotzdem auf ein viel fundamentaleres Phänomen hin.

Großbritannien, mit Küste (und Schnee)(Bild: Jeff Schmaltz, MODIS Rapid Response Team, Goddard Space Flight Center)

Ein Phänomen, das so interessant ist, dass der Mathematiker Benoît Mandelbrot im Jahr 1967 immerhin einen wissenschaftlichen Aufsatz mit dem Titel “How Long Is the Coast of Britain?” darüber veröffentlich hat. Darin beschreibt er den Prozess, mit dem man die Küstenlänge von Großbritannien bestimmen kann. Normalerweise würde man sich dazu einfach eine Landkarte nehmen oder noch besser, ein sehr genaues Satellitenfoto der Insel. Dann nimmt man ein Lineal, und misst einfach nach. Mit dem Maßstab der Aufnahme kann man dann die am Foto gemessene Länge leicht in die reale Küstenlänge umrechnen. Nur: Die Auflösung des Fotos ist begrenzt. Gehen wir mal davon aus, dass wir nur ein sehr ungenaues Bild haben und darauf keine Details zu sehen sind, die kleiner als ein Kilometer groß sind. Bei unserer Messung würden wir dadurch zwangsläufig alle Buchten, Fjorde und Unregelmäßigkeiten verpassen, die unter diese Schwelle fallen. Wenn die Küste von Großbritannien irgendwo einen kleinen Knick macht, der aufgrund der geringen Auflösung am Foto nicht zu sehen ist, dann würden wir dort einfach eine gerade Linie messen. Unsere gemessene Küstenlinie ist dann natürlich kürzer als die reale Küste. Wir brauchen ein genaueres Bild! Wenn wir jetzt eines haben, dass eine Auflösung von 10 Metern hat, können wir die Länge viel genauer messen. Mit dieser Auflösung wird die gemessene Küstenlänge deutlich größer sein als zuvor bei der Auflösung von 1000 Metern. Aber wir werden immer noch viele kleine Details verpassen und hätten wir ein Bild mit einer Auflösung von einem Meter benutzt, dann wäre die gemessene Länge noch größer.

Anders gesagt: Wie lang die Küste von Großbritannien ist, hängt vom Maßstab ab, den man verwendet. Das ist in gewissen Sinn natürlich immer noch eine dumme Aussage. Natürlich ändert sich die Geografie der Insel nicht, je nachdem wie ich sie betrachte. Die ist immer gleich. Und natürlich hat die Küste einer Insel keine fixe, klar definierte Länge. Und sie ist schon gar nicht unendlich lang. Denn das würde ja aus dem folgen, was ich gerade erklärt habe. Je kleiner der Maßstab ist, den man benutzt, desto länger wird die gemessene Küste – und ist der Maßstab irgendwann wirklich winzig, nähert sich die gemessene Länge einem unendlich großen Wert an. Aber die Küste von Großbritannien ist eben weder unendlich lang noch kann man eine eindeutige Länge bestimmen. Da gibt es Gezeiten, die mal mehr und mal weniger Land wasserfrei lassen; es gibt Wellen und spätestens wenn man zu sehr, sehr kleine Skalen geht, macht es keinen Sinn mehr, von einer fixen Länge zu besprechen. Dann reicht es schon, wenn jemand am Strand einen Kieselstein mit dem Fuß wegkickt um die Küstenlänge zu verändern.

Mandelbrot ging es auch um etwas anderes. Er betrachtete in seiner Arbeit eine mathematische Gleichung, die der englische Physiker Lewis Fry Richardson entdeckt hatte. Die Länge einer geografischen Grenze ist gleich einer Konstante M multipliziert mit dem bei der Messung verwendeten Maßstab hoch (1-D). Und dieses “D” ist es, worauf es ankommt. Wäre die Grenze eines Landes zum Beispiel eine gerade Linie, dann spielt es keine Rolle, welchen Maßstab man verwendet. Stellen wir uns ein Land vor, dessen Grenze ein Quadrat mit einer Seitenlänge von 100 Kilometern ist. Wenn wir eine Auflösung von 100 Kilometern verwenden, dann würden wir eine Grenzlänge von 400 Kilometern messen. Daran ändert sich aber auch nichts, wenn wir die Auflösung immer genauer machen. Die Länge bleibt immer gleich und in Richardsons Formel entspricht das einem Wert von D, der gleich 1 ist. Je komplizierter die Form der Grenze aber wird, je verschachtelter und in sich verschlungener, desto größer ist der Einfluss des bei der Messung verwendeten Maßstabs. Und desto größer wird der Wert für D in der Formel.

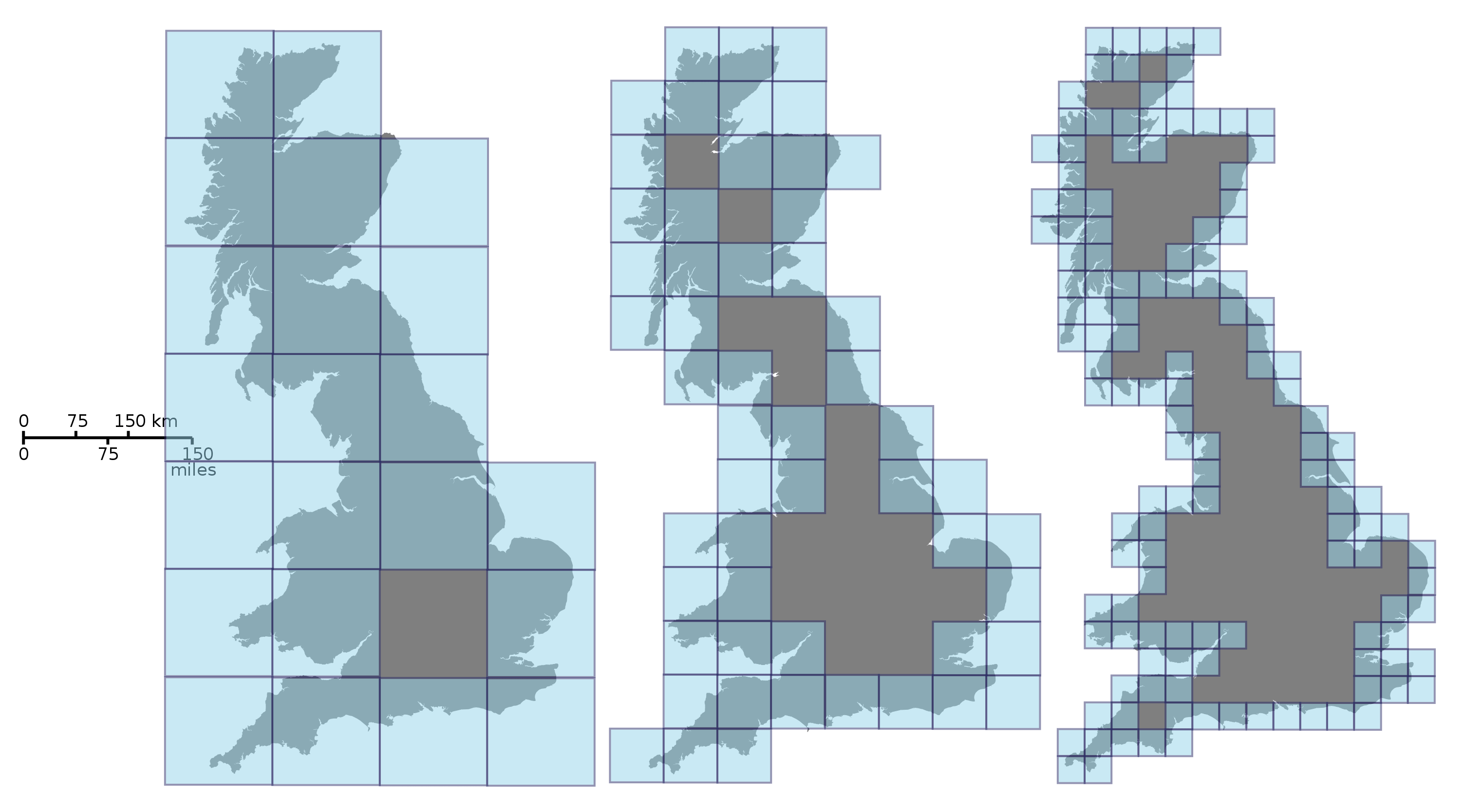
Je nachdem wie genau man schaut wir die Küste von Großbritannien länger… (Bild: Prokofiev, CC-BY-SA 3.0) Je nachdem wie genau man schaut wir die Küste von Großbritannien länger…
(Bild: Prokofiev, CC-BY-SA 3.0)

Dieses D ist das, was Mandelbrot später als “fraktale Dimension” bezeichnet hat. Über Dimensionen habe ich ja schon in Folge 267 der Sternengeschichten ausführlich gesprochen. Vereinfacht gesagt bezeichnet man damit die Menge an unterschiedlichen Richtungen im Raum. In unserem normalen Raum sind das drei Dimensionen. In einer Ebene gibt es zwei Dimensionen und auf einer Linie nur eine. Dort kann ich vor und zurück gehen, aber nicht rauf oder runter oder links bzw. rechts. Und deswegen bezeichnen wir eine Linie auch als eindimensionales Objekt. Das gilt auch für Linien, wie zum Beispiel die Küstenlinie von Großbritannien. Es ist eine Linie und so wie jede Linie sollte ihre geometrische Dimension gleich eins sein. Das ist sie natürlich auch – aber Mandelbrot fand einen Weg, wie man auch anders darüber nachdenken kann.

Die eindimensionale Linie einer Küste wie die von Großbritannien ist so sehr in sich selbst verschlungen und verschachtelt, dass sie bei bestimmter Betrachtung nicht mehr nur Eigenschaften einer Linie zeigt, sondern auch Eigenschaften einer Fläche. Man kann sich das so vorstellen, als wolle man ein Blatt Papier mit einem einzelnen Bleistiftstrich komplett anmalen. Selbst wenn man den Stift nie absetzt, kann man sich eine Linie denken, die sich so sehr hin und her windet und so sehr verschachtelt ist, dass am Ende das ganze Blatt voll gemalt erscheint. In der Realität ist ein Bleistiftstrich natürlich auch keine eindimensionale Linie sondern ein ausgedehnter, zweidimensionaler breiter Strich. Aber zumindest anschaulich ist es genau das, was Mandelbrot betrachtet hat: Manche Linien sind so komplex, dass sie Eigenschaften von Flächen annehmen und das zeigt sich an ihrer Dimension.

Zumindest dann, wenn man Dimension so auffasst, wie Richardson das mit seiner Formel getan hat. Denn die misst genau das, was ich gerade beschrieben habe. Für ein Land mit exakt geraden Grenzlinien ist es egal, welchen Maßstab man verwendet und die Konstante D, die “Dimension” der Linie, beträgt eins. Je komplexer die Grenze aber wird, desto mehr nähert sich der Wert von D der Zahl 2 an, als der Dimension, die wir einer Fläche zuschreiben. Für die Küstenlinie von Großbritanien kam Richardson so auf einen Wert von 1,25.

Man kann das Konzept auf eine andere Art leichter verstehen. Stellen wir uns vor, wir haben eine exakt gerade Linie, die genau einen Meter lang ist. Und ein Quadrat, das eine Länge von einem Meter hat. Wie viele Quadrate brauchen wir, um die Linie komplett damit zu bedecken? Genau eines natürlich. Jetzt halbieren wir die Länge des Quadrates – wie viele Quadrate brauchen wir nun? Genau doppelt so viele, nämlich zwei. Dritteln wir die Länge, brauchen wir drei Quadrate; wird sie geviertelt, brauchen wir vier – und so weiter. Die Anzahl der zur Überdeckung benötigten Quadrate steigt linear mit der Verkleinerung der Länge. Das gleiche Spiel können wir jetzt aber auch mit einer sehr verschachtelten Linie machen. Dann passiert das gleiche, was ich vorhin schon zur Messung der Küste Großbritanniens erzählt habe. Je kleiner wir die Quadrate machen, desto mehr davon brauchen wir auch hier, um die gesamte Linie zu bedecken. Aber weil die Linie hier eben sehr viel mehr Details hat, steigt die benötigte Anzahl nicht mehr linear, sondern viel stärker. Im Extremfall – der Linie, mit der wir ein komplettes Blatt Papier vollgemalt haben, steigt die Anzahl nicht mehr linear, sondern quadratisch. Soll heißen: Wenn wir ein Blatt Papier mit einem Quadrat komplett bedecken wollen, dann reicht auch hier ein Quadrat, sofern es so groß ist wie das ganze Blatt. Halbieren wir die Seitenlänge des Quadrats, brauchen wir dann aber nicht zwei davon, sondern vier wenn wir alles abdecken wollen. Und vierteln wir die Länge, sind nicht vier, sondern 16 Quadrate nötig – und so weiter. Mathematisch gesehen kann man das mit einer Formel wie der von Richardson aufschreiben, bei der eine Zahl D auftaucht, die im linearen Fall gleich 1 ist und im quadratischen Fall gleich 2. Oder anders gesagt: D entspricht der Dimension des Objekts das wir betrachten und so wie wir es erwarten ist dann auch hier die Dimension einer geraden Linie gleich 1 und die einer Ebene bzw. Fläche gleich 2.

Mandelbrot bewies die Schönheit der Mathematik

Aber, und das ist die nette Idee von Mandelbrot, wer sagt denn, das man nicht auch Zahlen betrachten kann, die zwischen 1 und 2 liegen? Wer sagt denn, dass eine Dimension immer eine ganze Zahl sein kann? Spielt man das Spiel mit der Überdeckung mit der Linie, die die Küste von Großbritannien darstellt, dann erhält man als Ergebnis eben weder 1 noch 2, sondern etwas dazwischen. Solche Dimensionswerte, die keine ganzen Zahlen sind, hat Mandelbrot “fraktale Dimensionen” genannt und es gibt für sie jede Menge Anwendungen.

Zum Beispiel immer dann, wenn man eine Möglichkeit sucht, um die Form von Dingen zu beschreiben. Etwa die Form von Einschlagskratern. Wenn die frisch sind, dann sind die Grenzen der Krater sehr klar und scharf und sehr komplex. Je länger ein Krater existiert, desto stärker kann die Erosion wirken und die vielen Details verschwinden. Bestimmt man also die fraktale Dimension der Linie, die einen Einschlagskrater begrenzt, dann ist sie um so größer, je jünger der Krater ist. Die fraktale Dimension kann aber auch verwendet werden, um Sonnenflecken zu beschreiben oder die Form von kosmischen Staubteilchen. Sie spielt eine Rolle, wenn man die Dynamik von Himmelskörpern verstehen will – und das waren jetzt nur ein paar der astronomischen Anwendungen.

Fraktaler Romanesco
(Bild: Jon Sullivan, public domain)

In der Mathematik ist die fraktale Dimension noch viel wichtiger. Hier braucht man sie, wenn man sich mit Chaostheorie beschäftigt; oder wenn man Computerprogramme schreiben will, die automatisch real aussehende Landschaften konstruieren. Denn die Küstenlinien sind nicht die einzigen in der Natur auftauchenden Objekte, die fraktale Eigenschaften haben. Das trifft auch für die Form von Wolken zu – oder zum Beispiel auch für Blumenkohl oder Romanesco. Gerade bei diesem Gemüse sieht man es besonders gut. Betrachtet man einen kleinen Teil des Romanesco – eine der Sproßen (heißen die Sproßen? Keine Ahnung…) – dann sieht der kleine Ausschnitt so aus wie das große Ganze. Und wenn man das Ding noch näher betrachtet, dann sieht der kleinere Ausschnitt wieder so aus wie der große. Das Phänomen nennt man “Selbstähnlichkeit” und es ist quasi das, was Fraktale so besonders macht. Wenn man das gleiche Ausmaß an Komplexität findet, egal wie genau man hin sieht, dann ist es kein Wunder, wenn man mit simpler Geometrie nicht mehr weiter kommt sondern ein neues Konzept braucht. In der Natur ist das Ausmaß an möglichen Stufen der Vergrößerung begrenzt. Irgendwann betrachte ich dann keinen Romanesco mehr, sondern nur noch Zellen, Moleküle und Atome. Aber in der puren Welt der Mathematik kann man Objekte konstruieren, die wahrhaft selbstähnlich sind, und bei denen man bis in alle Ewigkeit tiefer und genauer hinsehen kann, und trotzdem immer das gleiche Ausmaß an Komplexität findet. Aber das ist ein Thema für eine andere Folge der Sternengeschichten. 

Florian Freistetter promovierte am Institut für Astronomie der Universität Wien und hat danach an der Sternwarte der Universität Jena und dem Astronomischen Rechen-Institut in Heidelberg als Astronom gearbeitet. Zur Zeit lebt er in Baden bei Wien, bloggt über Wissenschaft, schreibt Bücher und ist Teil des Wissenschaftskabaretts Science Busters.

Fraktale: Die Faszination der verborgenen Dimension

.

(mfe)

Source: Sternengeschichten Folge 281: Fraktale Dimensionen
https://www.youtube.com/watch?v=lO1B2uA4l38